< link link link >

    Plattledningen består av två parallella metallplattor eller band med bredden a och plattavståndet b. Vi förutsätter, att a >>b samt att

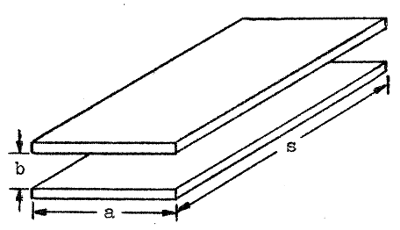		ledningslängden s >> a, vilket innebär, att fältet mellan plattorna kan anses homogent samt att fältet utanför plattsystemet kan försummas (jämför förhållandet i fråga om en plankondensator).     Vid radiofrekvens kan vi med ledning av sambanden J1.32 (sid. J1.10) och J1.40 (sid. J1.12) normalt förutsätta att
Plattledningen J3.1

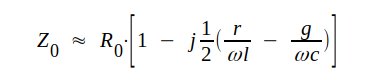	J3.1
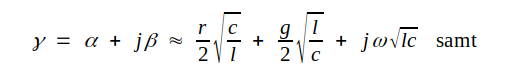	J3.2
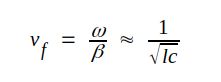	J3.3
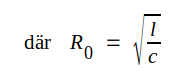	J3.4

    Här är l yttre induktansen per längdenhet, enär frekvensen förutsättes så hög, att vi har en utpräglad strömförträngning. Denna medför, att r ökar med frekvensen, dock på ett sådant sätt att r/ωl (liksom g/ωc) normalt avtar med frekvensen. Vid hög radiofrekvens och vid relativt små värden på r och g kan vi i de flesta fall klara oss med approximationen

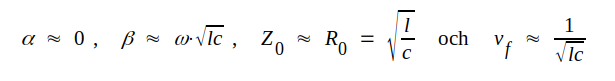J3.5

d.v.s. vi kan i många fall betrakta den förlustfria ledningen som en god modell av radiofrekvensledningen.

    Enligt tabellen (fig. J1.7) sid. J1.10 gäller för plattledningen

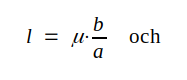	J3.6
	J3.7

Övning: Härled sambanden J3.6 och J3.7

    Insättes sambanden J3.6 och J3.7 i sambanden J3.5 får vi

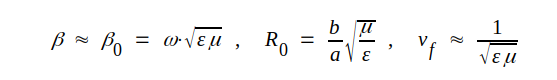J3.8

där vi infört den nya beteckningen β₀. Med ε = ε_r ε₀ och μ = μ_r μ₀ fås

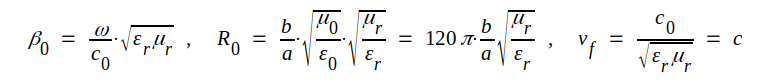J3.9

där 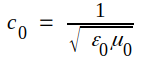 = ljushastigheten i vakuum (μ≈3·10⁸ m/s) och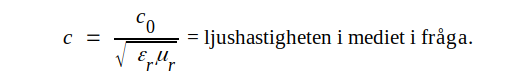


    Faskonstanten, fashastigheten och egenresistansen beror samtliga av isolermaterialets elektriska (ε_r) och magnetiska (μ_r) egenskaper. De båda förstnämda (β₀ och v_f) beror ej av ledningens geometriska dimensioner (a och b), vilket däremot egenresistansen R₀ gör. R₀ är i motsats till β₀ oberoende av frekvensen. De nämda egenskaperna gäller med god approximation för alla typer av parledningar vid radiofrekvens.

Övning: Studera tabellen sid. J1.10 i belysning av ovanstående påståenden. Beräkna faskonstant och fashastighet för de olika ledningstyperna.

link >