< link link link >

    En förlustfri plattledning matas i närändan av en generator med emk:n e = │E│⋅ sinωt. Vi räknar med sinusformat stationärt tillstånd och använder därför jω-metoden vid studium av vågutbredning på ledningen.

    Ledningens läge i rummet definieras av rymdkoordinatsystemet x-y-z. Nedre plattans översida benämner vi i fortsättningen golv och övre plattans undersida tak. Eftersom metallen förutsättes ideal (förlustfri ledning), blir strömförträngningen utpräglad, d.v.s. strömmen kan anses koncentrerad till golvets respektive takets ytskikt.

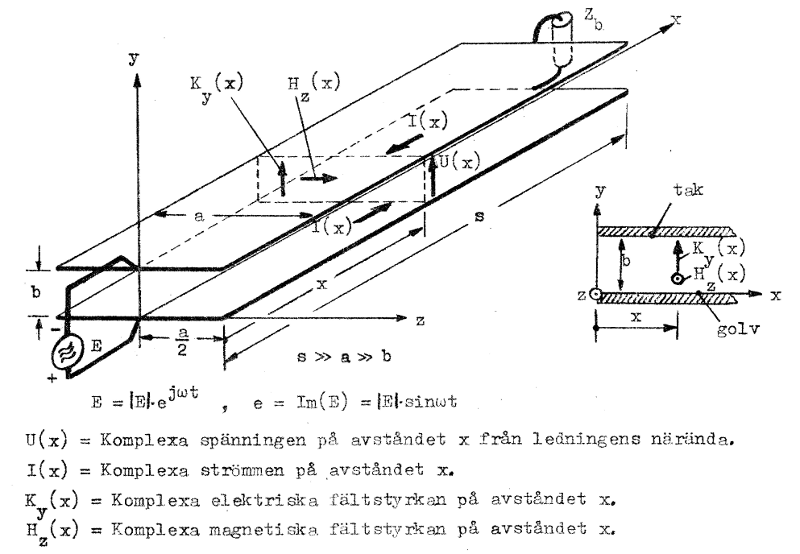
    Vi förutsätter, att vågutbredningen sker i ledningens längdriktning (x-riktningen), innebärande att fältet är homogent i varje plan x, d.v.s. beroende av x men oberoende av y och z. Det torde för läsaren vara uppenbart, att den elektriska fältvektorn mellan plattorna endast har en komponent i y-riktningen. Denna enda kompnent betecknar vi i komplex form med K_y(x). Den magnetiska fältvektorn har endast en komponent i z-riktningen, H_z(x). Se härtill fig. J3.2, där förutsättningar och beteckningar sammanfattas.

	Plattledningen jämte storhetsbeteckningar Fig. J3.2

    Skall fältet vara homogent i planet x=0, måste matningen ske längs hela ledningsbredden a och ej i två punkter, vilket fig. J3.2 visar. Liknande synpunkter kan läggas på belastningens inkoppling. Som alternativ till fig. J3.2 kan vi tänka oss två parallella i alla riktningar utsträckta ledande plan (golv och tak), som vi matar med en "oändligt lång generator" i planet x = 0. Vi utväljer sedan en kanal med bredden a och studerar utan randeffekter vågutbredningen i denna.

    Härledning av spännings- och strömfördelning på plattledningen följer samma schema som i tidigare avsnitt (se avsnitt J1.03, sid. J1.2) och upprepas därför ej här. Hänvisande till sambanden J1.13-14 (sid. J1.5) sammanfattar vi här resultaten.

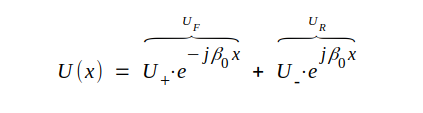	J3.10
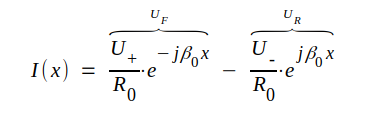	J3.11
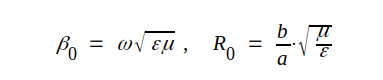	J3.12

    Sambandet J3.12 är en upprepning av J3.8. U_F och U_R respektive I_F och I_R är våra tidigare beteckningar för fram- och återgående spännings- respektive strömvåg. U₊ och U_- är godtyckliga konstanter, som bestämmes från fall till fall med ledning av det aktuella problemets randvillkor.

    Med ledning av nedanstående figurer undersöker vi nu sambanden mellan fältstorheterna och spänning-ström-storheterna.

Fig. J3.3	Fig. J3.4

    Eftersom det elektriska fältet är homogent i varje plan x, följer av fig. J3.3 att

J3.13

    Tillämpar vi Amperes lag (som här gäller, eftersom inget elektriskt fält passerar igenom integrationskonturen) i fig. J3.4, får vi ett mot sambandet J3.13 svarande samband för det magnetiska fältet, nämligen

J3.14

    Insättning av sambanden J3.13 och J3.14 i sambanden J3.10-11 ger:

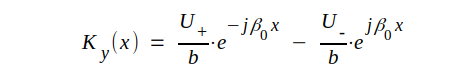	J3.15
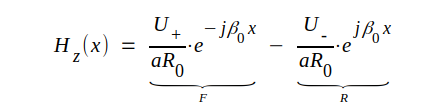	J3.16

    Vi inför nya godtyckliga konstanter via beteckningarna


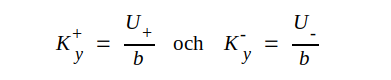    Härav följer att


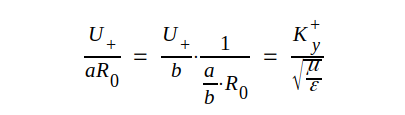där det sista ledet följer av sambandet J3.12. På analogt sätt får vi


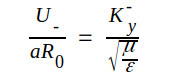    Slutligen inför vi

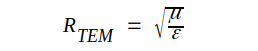J3.17

    Indexbeteckningen TEM kommer nedan att få sin förklaring.

    Med ovan införda beteckningar får sambanden J3.15-16 formen:

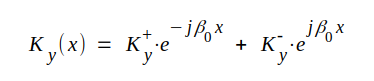	J3.18
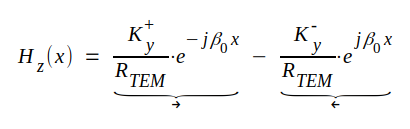	J3.19
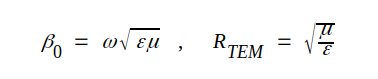	J3.20

    Här är alltså K⁺_y och K^-_y nya godtyckliga konstanter, som bestämmes av ledningens randvilkor.

    Pilarna i sambanden J3.18-19 betecknar framgående och återgående (reflekterad) våg liksom i sambanden J3.15-16 och J3.10-11.

    Det är instruktivt att studera den framgående vågen (eller den återgående) separat. Låt oss därför anta, att plattledningen är anpassad i sin fjärrända. Under denna förutsättning blir som bekant U- och därmed K^-_y lika med noll. Vid anpassad plattledning gäller alltså:

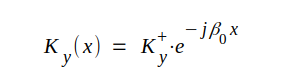	J3.21
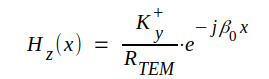	J3.22

    Innan vi närmare diskuterar den framgående vågens egenskaper bestämmer vi konstanten K⁺_y. För x = 0 är U(0) = E = │E│⋅e^jωt och i sambandet J3.21 är K_y(0) = K⁺_y. Enligt sambandet J3.13 får vi

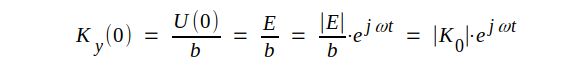J3.23

där vi infört │K₀│= │E│/b = den elektriska fältstyrkans toppvärde i planet x = 0. I det fall vi studerar (anpassad ledning) har för övrigt elektriska fältstyrkan detta toppvärde överallt på ledningen, eftersom den är förlustfri och eftersom reflekterad våg saknas.

    Med sambandet J3.23 får sambanden J3.21-22 formen:

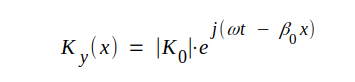	J3.24
	J3.25

    Motsvarande momentanvärden blir

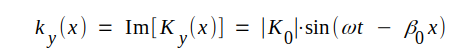	J3.26
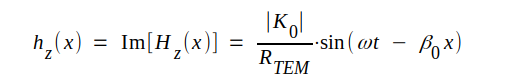	J3.27

    Sambanden J3.24-27 jämte sambanden J3.20 sammanfattar några mycket väsentliga egenskaper hos det i plattledningen forskridande fältet.

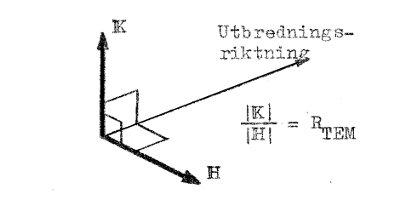		Fältvektorerna K och H är intimt förknippade med varandra och kan för övrigt aldrig existera oberoende av varandra i tidsvariabla fält. Vi säger, att en elektromagnetisk våg utbreder sig mellan golv och tak i plattledningen. Fältvektorerna är båda vinkelräta (transversella) mot utbredningsriktningen. Vågen säges
TEM-vågens fundamentala egenskaper Fig. J3.5

därför vara en TEM-våg (Transversell Elektriskt och Magnetiskt). Vi observerar också, att fältvektorerna är vinkelräta mot varandra. Se härtill fig. J3.5.

    Fältvektorerna i den fortskridande vågen står i det konstanta förhållandet R_TEM till varandra, en fundamental egenskap hos fältet, eftersom R_TEM är oberoende av plattledningens dimensioner. R_TEM, som har sorten ohm, benämner vi vågimpedans eller här alternativt vågresistans, enär R_TEM är en reell storhet. Vi har generellt

J3.28

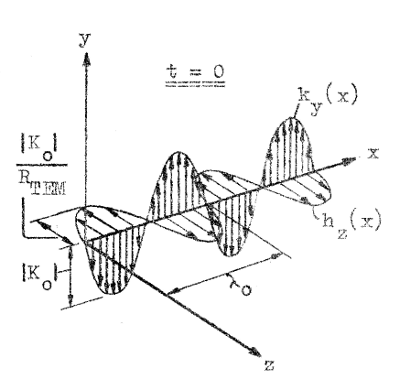
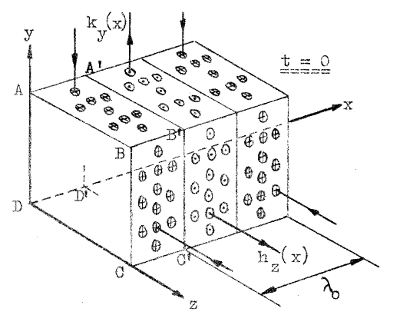
     I fig. J3.6 och J3.7 har vi på två olika sätt och med ledning av sambanden J3.26-27 sökt klargöra TEM-vågens "utseende" vid en viss tidpunkt (för enkelhets skull t=0).

TEM - vågen Fig. J3.6	TEM - vågen Fig. J3.7

    Fig. J3.6 representerar ett vanligt ritsätt, som här lämnas utan komentar. I fig. J3.7 tänker vi oss, att vi ur fältet skurit ut en parallellepipedisk låda, varefter vi ritat in de elektriska och magnetiska fältlinjernas skärningspunkter med lådans sidoytor. Fältlinjernas täthet får därvid representera fältstyrkornas storlek. I ytorna ABCD, A'B'C'D' o.s.v. finns inget fält. I varje plan parallellt med ytan ABCD är fasen konstant och fältvektorerna ligger i detta plan, som är vinkelrätt mot utbredningsriktingen. Ett dylikt plan säges utgöra en vågfront. Vågor med plan vågfront benämnes plana vågor.

    Om elektriska fältstyrkevektorn i en elektromagnetisk våg ligger i ett vertikalplan, säges vågen vara vertikalt polariserad; ligger den i ett horisontalplan säges vågen vara horisontalt polariserad. Planet genom vektorn Ҝ och fortplantningsriktningen brukar benämnas polarisationsplanet.

     Enligt sambanden J3.26-27 är såväl k_y(x) som h_z(x) konstanta, om ωt - β₀x = konstant. Detta fordrar, att x ökar i takt med tiden t, d.v.s. vågbilden enligt fig. J3.6 eller J3.7 rör sig i x-axelns positiva riktning med sådan hastighet, att ωt - β₀x = konstant.

    Vi deriverar sambandet ωt - β₀x = konstant med avseende på tiden och får


      är vår tidigare introducerade fashastighet (vf). Se härtill avsnitt J1.06, sid. J1.10. Vår i avsnitt J1.08 (sid. J1.14) introducerade grupphastighet blir


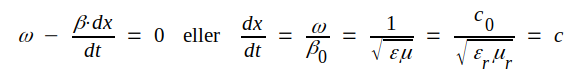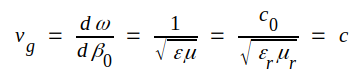d.v.s.

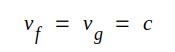J3.29

där 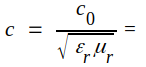 ljushastigheten i mediet i fråga. c₀ = ljushastigheten i vakuum (luft).

    Eftersom faskonstanten β₀ är fasvridningen per längdenhet följer direkt att (se fig. J3.6-7)


där λ₀ = våglängden. Vi får


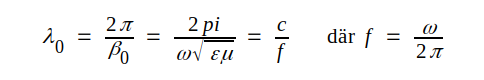    Alltså

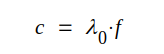J3.30

    Eftersom c < c₀ blir vid fix frekvens våglängden i ett fast isolermaterial kortare än i vakuum.

    Vi har ovan konstaterat, Att TEM-vågens egenskaper helt karakteriseras av RTEM och β₀ , vilka båda endast beror av det medium, i vilket TEM-vågen utbreder sig. Detta låter oss förmoda, att TEM-vågen är av mera fundamental natur än ovanstående framställning visar. Sålunda kan den elektromagnetiska våg, som utstrålas från en antenn, betraktas som en plan TEM-våg på stort avstånd från antennen. Är strålningskällan punktformad blir vågfronten kotformad, men på stort avstånd från källan (antennen) är vågfrontens krökning så liten, att den kan betraktas som närmelsevis plan inom ett mindre område.

link >