< link link link >

    Låt oss beräkna den effekt P, som den framgående vågen överför. För denna har vi enligt sambanden J3.24-25:


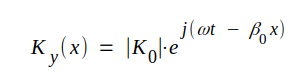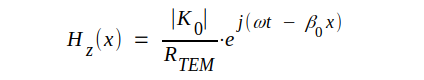    Enligt sambanden J3.13 och J3.14 är vidare


    Eftersom U(x) och I(x) är i fas med varandra, får vi direkt


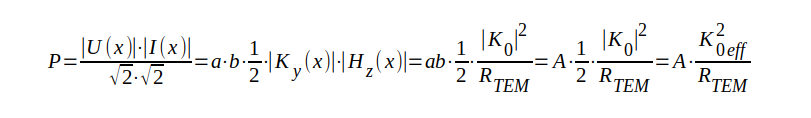    Vi inför nu strålningsstyrkan S (=överförd effekt per ytenhet vinkelrätt mot utbredningsriktningen) och får

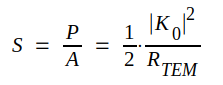J3.31

    Eftersom 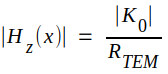 inför vi i analogi med beteckningen │K₀│ beteckningen 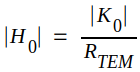 magnetiska fältstyrkans toppvärde. Därmed får vi följande tre alternativa skrivsätt för strålningsstyrkan S.

J3.32

    Ett annat vid beräkningar praktiskt sätt att skriva uttrycket på S är följande.

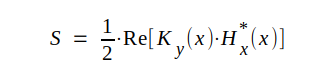J3.33

där H^*_z(x) är den till H_z(x) konjugerade komplexa storheten.

Anmärkning 1: Lägg i sambanden J2.32 märke till likheten med de kända effektformlerna: P = U²_eff / R = U_eff · I_eff = R²_eff, där I_eff är ström genom och U_eff spänning över en resistans R.

Anmärkning 2: Sambandet J3.33 är motsvarigheten till den vid jω-metoden ofta använda effektformeln: .

    Enligt vanligt språkbruk säger vi, att energi överföres från en plats till en annan via en ledning, utan att vi närmare tänker på var energien går fram. Räkningen lvan gör det naturligt att tänka sig det elektromagnetiska fältet som bärare av energien, medan själva ledningen (i förlustfallet) endast åstadkommer en oundviklig energiförlust. Däremot kan vi säga, att ledningen leder energien i en bestämd riktning och i denna bemärkelse är varje ledning en "vågledare".

    Effektransporten säges ske genom strålning och vår ovan beräkande effekt P kan vi därför lämpligen benämna strålningseffekt.

    Vi refererar i vågutbredningssammanhang ofta till den s.k. Poynting's strålningsvektor S, som är en vektor, lagd i effekttransportriktningen (utbredningsriktningen) och med absolutbeloppet lika med strålningsstyrkan S.

    Vi har ovan förutsatt en framgående våg på ledningen, d.v.s. vi har förutsatt, att plattledningen har varit anpassad i fjärrändan. Belastningen Z_b (se fig. J3.2) har med andra ord haft värdet


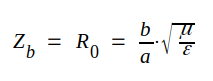    För att få anpassning kan vi knappast låta Z_b var ett diskret impedanselement på sätt som fig. J3.2 visar, ty fältbilden måste i så fall bli deformerad, eftersom vi tvingar strömlinjerna i plattorna att avvika in mot belastningsimpedansens anslutningspunkter.

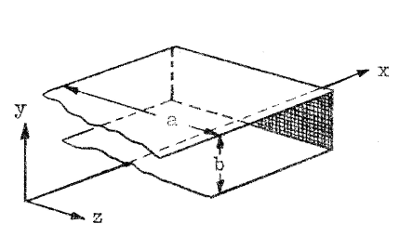		Vi låter i stället belastningen utgöras av ett mycket tunt resistivt skickt (en s.k. resistansfilm), t.ex. en metalliserad isolatoryta, placerad vineklrätt mot x-axeln (se fig. J3.8) och med dimensionerna a gånger b. Strömlinjerna i filmen kan då antas gå i y-ritkningen.
Fig. J3.8
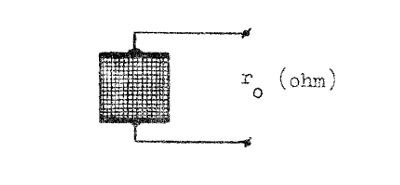		Vi definierar resistansfilmens ytrestivitet r0 (ohm) som resistansen mellan två motstående sidor hos ett kvadratiskt filmskikt. Se härtill fig. J3.9.
Fig. J3.9

Övning: Visa att r₀ är oberoende av storleken på resistanskvadraten.

    Resistansen hos den i plattledningens fjärrända placerade resistansfilmen blir


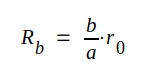    Ytresistiviteten väljes nu så, att plattledningen blir anpassad, d.v.s. så att

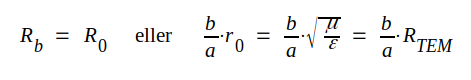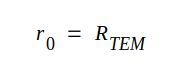J3.34

    Ytresistiviteten skall alltså väljas lika med vågresistansen. Under denna förutsättning uppsuges den framgående vågen helt av resistansfilmen.

Övning: Visa att 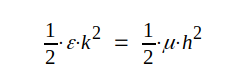 , där k och h är elektriska respektive magentiska fältstyrkans momentanvärde. Vilka slutsatser kan man dra av den nämnda likheten?

link >