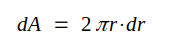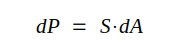< link link link >

    För den teoretiskt intresserade ges nedan en kort behandling av koaxialledningens väsentliga egenskaper. Fö koaxialledningen är, liksom för alla parledningar, TEM-vågen den s.k. grundvågen, vilken definieras som den för ifrågavarande ledning möjliga vågtyp, som har den lägsta gränsfrekvensen (lägsta möjliga överföringsfrekvensen). Alla parledningar kan överföra likström och har därför gränsfrekvensen noll. TEM-vågen är koaxialledningens normala vågtyp, med det bör beaktas att andra vågtyper kan förekomma på en koaxialledning, något som dock förbigås här.

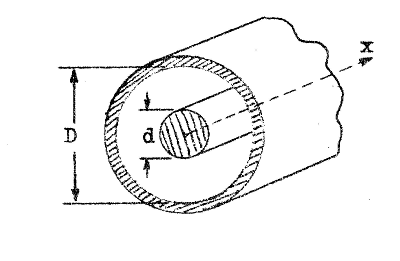		Koaxialledningen utgöres av en rörformig, metallisk ytterledare (innerdiameter D) och en med denna koncentrisk innerledare (ytterdiameter d). Utrymmet mellan ledarna utfylles av ett dielektrikum, som kan vara luft. Är koaxialledningen böjlig benämnes den koaxialkabel. Se härtill fig. J3.11.
Koaxialledningen J3.11

    Liksom i fråga om plattledningen kan vi vid hög radiofrekvens i några fall betrakta koaxialledningen som praktiskt taget förlustfri, d.v.s. vi sätter

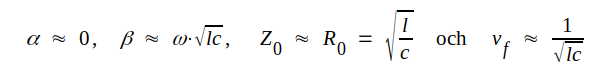J3.35

    Enligt tabellen (fig. J1.7I sid. J1.10 gäller för koaxialledningen

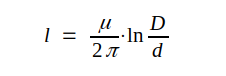	J3.36
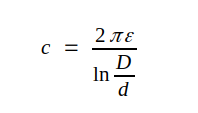	J3.37

Övning: Härled sambanden J3.36 och J3.37.

    Insättes sambanden J3.36 och J3.37 i sambanden J3.35 får vi

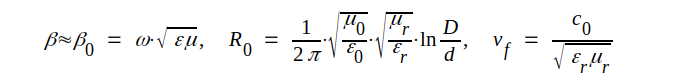J3.38

    β₀ bestämmer vågutbredningen längs den förlustfria ledningen (x-riktningen), men vi vet ej hur det elektromagnetiska fältet fördelar sig över koaxialledningens tvärsnitt. Att besvara denna fråga är vår närmaste uppgift.

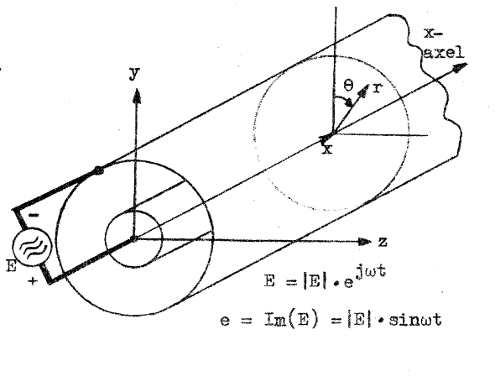		Vi antar, att ledningen matas i planet x = 0 av en emk e = │E│·sinωt (fig. J3.12). Vi antar tills vidare, att ledningen är oändligt lång och vi begagnar jω-metoden vid våra beräkningar.     Koaxialledningen i fig. J3.12 inlagts i ett x-y-z-koordinatsystem. Eftersom ledningen har cylindrisk symmetri är det lämpligare att låge en punkt i ledningen
Fig. J3.12

definieras av koordinaterna r, θ och x (cylinder-koordinater; som längdkoordinat i fråga om cylinderkoordinater användes normalt beteckningen z, men vi begagnar som tidigare beteckningen x). De tre koordinaterna r, θ och x definierar i varje punkt tre mot varandra vinkelräta axelriktningar.

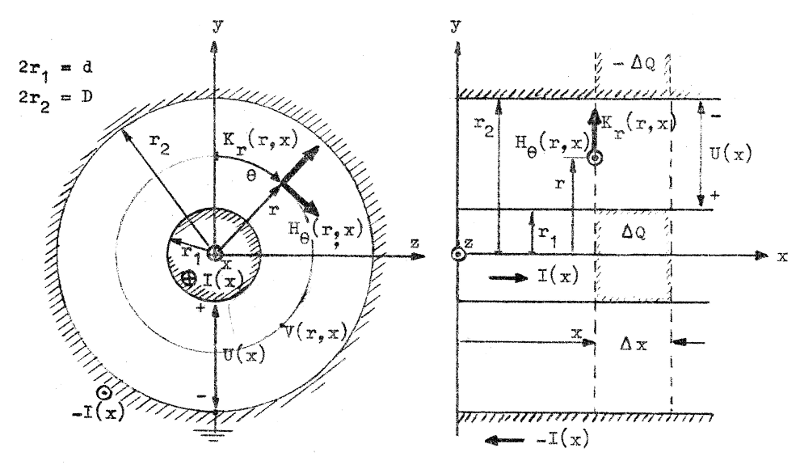
    Av symmetriska skäl är det elektriska fältet i ett godtyckligt plan x radiellt d.v.s. det har endast en komponent i r-riktningen. Vi betecknar denna elektriska fältstyrka (komplex form) K_r(r,x), eftersom den bör vara en funktion av x och r. Av symmetriskäl är den däremot oberoende av koordinaten θ. Det magnetiska fältet har av symmetriskäl endast en fältstyrkekompnent i θ-riktningen. Vi betecknar denna med H_θ(r,x). Se härtill fig. J3.13 nedan.

	Koaxialledningens storheter Fig. J3.13

    Vi betraktar en "dosa" med tjockleken Δx och radien r. Betecknas den elektriska flödestätheten på dosans cylindriska vägg med D_r(r,x) blir totala flödet genom denna vägg


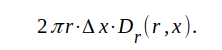     Eftersom inget elektriskt flöde passerar genom dosans gavlar, blir enligt flödessatsen det ovan beräknade flödet lika med den i dosan inneslutna laddningen, som betecknas ΔQ. På ytterledaren finns på sträckan Δx givetvis laddningen -ΔQ. Vi får sålunda

J3.39

d.v.s

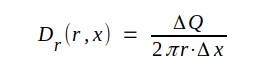J3.40

     Härav följer att

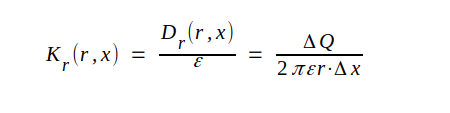J3.41

    I fig. J3.13 observerar vi, att U(x) är komplexa spänningen mellan ledarna, medan V(r,x) är komplexa potentialen på en godtycklig cylinder med radien r. Låter vi godtyckligt potentialen vara noll på ytterledaren (r = r₂ = D/2), får vi alltså:


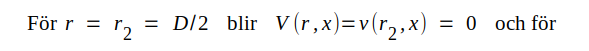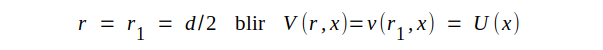    Som en följd av definitionen för elektrisk fältstyrka går vi vidare

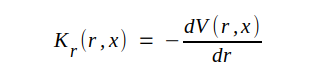J3.42

eller


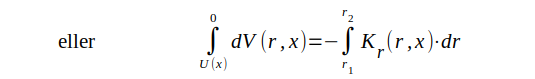som med sambandet J3.41 ger

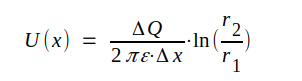J3.43

    Med hjälp av sambandet J3.43 kan uttrycket för komplexa elektriska fältstyrkan (J3.41) skrivas på följande sätt.

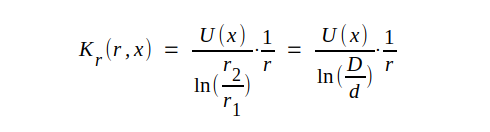J3.44

    För beräkning av magnetiska fältstyrkan tillämpar vi Ampers's lag och får

J3.45

där integrationsvägen är en cirkel med radien r i planet x (se fig. J3.13). Inget elektriskt flöde passerar genom den valda integrationsslingan, vilket är förutsättningen för giltigheten hos Ampere's lag.

    Alltså blir

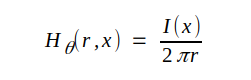J3.46

    K_r(r,x) och H_θ(r,x) är vinkelräta mot varandra och kvoten mellan dem blir:

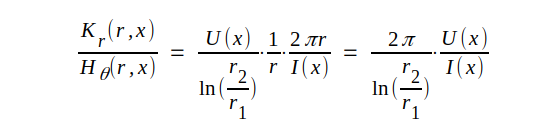J3.47

    Eftersom vi enligt vårt tidigare antagande (sid. J3.12) betraktar en oändligt lång ledning är U(x) och I(x) komplex spänning respektive ström hos en framgående våg, d.v.s. vi har

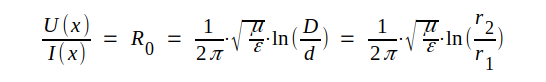J3.48

    Med J3.48 får vi ur sambandet J3.47

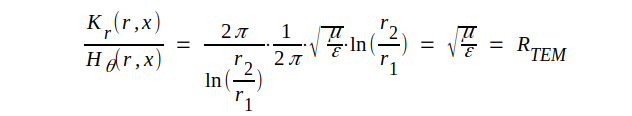J3.49

    Av våra hittillsvarande räkningar framgår att fältvektorerna K och H har de egenskaper, som karakteriserar TEM-vågen (punkterna 1 till 4 i sammanställningen på sid. J3.11).

    Låt oss så notera det fullständiga uttrycket på fältkomponenterna i den fortskridande vågen, då ledningen enligt fig. J3.12 matas i näränden med emk:n emk:n e = │E│⋅ sinωt. Eftersom ledningen är förlustfri och eftersom vi studerar en framgående våg, vet vi av erfarenhet av tidigare räkningar att

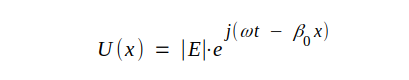J3.50

    Härav följer efter insättning i sambanden J3.44 och J3.49 att

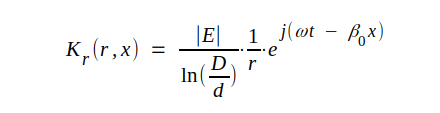	J3.51
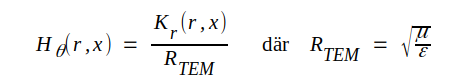	J3.52

    De mot J3.51 och J3.52 svarande momentanvärdena k_r(r,x) och h_θ(r,x) utgör imaginärdelarna av K_r(r,x) respektive H_θ(r,x).

    Låt oss slutligen beräkna den strålningseffekt, som den framgående vågen överför. Vi beräknar strålningsstyrkan S med ledning av sambandet J3.33 (sid. J3.9) och får (effekten kan beräknas på enklare sätt men ur övningssynpunkt går vi vägen över sambandet J3.33).


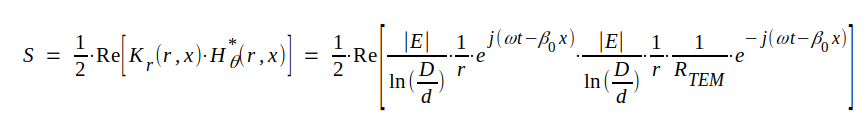som efter förenkling ger:

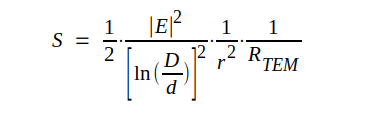J3.53

    Strålningsstyrkan S är som synes en funktion av r och vi måste därför beräkna totala strålningseffekten P genom integration. Som integrationselement

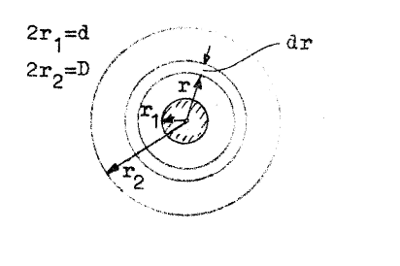		väljer vi en cirkulär ring med radien r och bredden dr enligt fig. J3.14. Det ringformade elementet har arean     Strålningseffekten genom elementet blir sålunda
Fig. J3.14

     Vi får sålunda

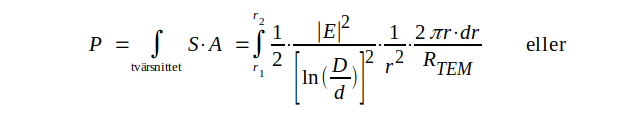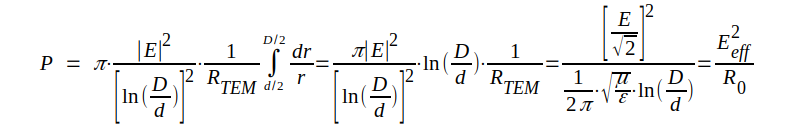J3.54

där sista ledet följer av sambandet J3.38.

    Effektuttrycket kan som tidigare nämnts beräknas på ett betydligt enklare sätt. Eftersom ledningen antagits oändligt lång, är dess inimpedans R₀, varför generatorn matar in effekten


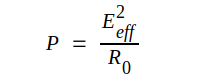    Strålningseffekten är densamma i varje tvärsnitt, eftersom ledningen antagits sakna förluster.

    Effektberäkningen ovan står i full överensstämmelse med punkt 5 i sammanfattningen på sid. J3.11.

Övning: Visa att koaxialledningen (i överensstämmelse med punkt 6 i sammanfattningen på sid. J3.11) blir anpassad, om den i sin fjärrända avslutas med en plan resistiv skiva med ytresistiviteten . Skivan är vinkelrät mot koaxialledningens längdaxel (x-axel) och förbinder inner- och ytterledare med varandra.

Övning: Härled primärkonstanten c ur sambandet J3.43.


link >