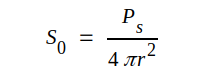< link link link >

    Efter att ha studerat TEM-vågens väsentliga egenskaper kan vi lämpligen beröra några elementära men viktiga antennbegrepp, vars innebörd vi kan förstå utan att fördjupa oss i antenteori.

    En antenn har till uppgift att utsända elektromagnetisk strålning (sändarantenn) eller att mottaga dylik strålning (mottagarantenn). Av antennen kräver vi oftast viss riktverkan. Normalt är antennen ansluten till en transmissionsledning, som för effekt till eller från antennen. Vi kan därför även se antennen som ett anpassningsdon mellan ledningen och fria rummet (tomrummet). I denna sin egenskap är antennen (liksom exempelvis en anpassningstransformator) reciprok, av vilket bland annat följer att antennens riktegenskaper är likadana, då man använder den för sändning som då man använder den för mottagning.

    Med en isotrop antenn (isotrop strålare) menar vi en antenn, som fördelar strålningen jämnt i alla riktningar. På konstant avstånd från antennen (d.v.s. på en klotyta med den isotropa antennen i centrum) är strålningstyrkan överallt konstant. En dylik antenn existerar ej i sinnevärlden, men begreppet isotrop antenn har i egenskap av referens stor betydelse i antennteoretiska sammanhang.

		Om en isotrop antenn utstrålar effekten (strålningseffekten) Ps, så fördelas denna likformigt över en klotyta (area 4πr2) d.v.s. strålningsstyrkan (jämför sid. J3.9) på avståndet r från antennen (se fig. J3.15 blir J3.55
Isotrop strålare Fig. J3.15

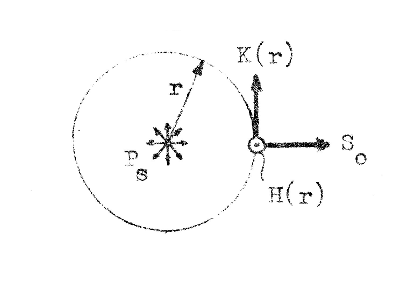
    Den isotropa antennen utstrålar en sfärisk våg; vågfronterna utgöres av sfärer med antennen i centrum. På stort avstånd från antennen ( r >> λ₀; antennens s.k. strålningszon) upplever en betraktare vågfronten som praktiskt taget plan och det är därför rimligt att förutsätta, att den utstrålade vågen kan betraktas som en plan TEM-våg med alla de egenskaper, som vi tidigare härlett och sammanfattat i avsnitt J3.05 (sid. J3.11).

    Om TEM-vågens komplexa elektriska och magentiska fältstyrka betecknas K(r) respektive H(r), får vi med utnyttjande av sambanden J3.32 och J3.55

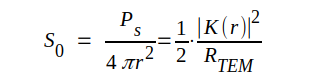	J3.56
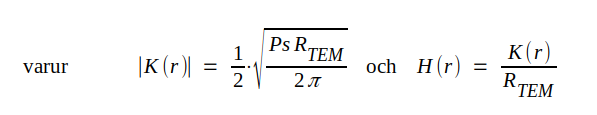	J3.57

     Den elektriska (och därmed även den magnetiska) fältstyrkans amplitud är sålunda omvänt proportionell mot avståndet till sändarantennen. Vid tillämpning av sambandet J3.57 får vi ej glömma, att vi förutsatt, att antennen befinner sig i tomrummet. Sambandet tar ej hänsyn till inverkan av antennen närbelägna föremål (markytan, metalliska reflektorer).

    Om en verklig antenn har riktverkan, så har den också en maximal strålningsriktning, i vilken strålningsstyrkan är störst (S_max i fig. J3.16)

	Strålning från antenn med riktverkan Fig. J3.16

     Begreppet direktivitet D för en antenn definieras på följande sätt:

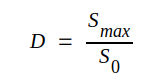J3.58

där
      S_max  = strålningsstyrkan i maximalstrålningsriktningen på avståndet r ( r >> λ₀) från antennen, då denna utstrålar effekten P_s.
      S₀      = strålningsstyrkan på samma avstånd r från en isotrop antenn, som utstrålar ovannämnda effekt P_s. S₀ kan alltså beräknas ur sambandet J3.55.

    Direktiviteten anges ofta i dB och vi har då sambandet

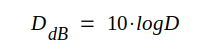J3.59

där D_dB = direktiviteten uttryckt i dB.

    På grund av oundvikliga förluster i antennen är i allmänhet antennens utstrålade effekt P_s något mindre än antennens tillförda effekt P. Antennens strålningsverkningsgrad η_s definierar vi som kvoten

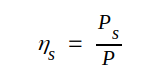J3.60

    I antenntekniken inför man även begreppet antennförstärkning, som definieras

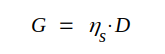J3.61

    Även antennförstärkningen G anges ofta i dB. Vi har då

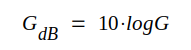J3.62

     Då en antenn användes som mottagarantenn bör rimligtvis effekten P_m i den till antennen anslutna belastningen (mottagaren) bli proportionell mot strålningsstyrkan S hos den mot antennen infallande vågen, d.v.s. vi har P_m = A ⋅ S, där A är en konstant, som får dimensionen yta. Vi definierar en antenns absorptionsarea (absorptionsyta) A på följande sätt.

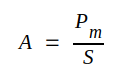J3.63

där

        P_m = effekt i en till antennen ansluten och anpassad belastning, då antennen är orienterad på bästa sätt (så att P_m = maximum) i förhållande till en mot antennen infallande TEM-våg.

        S   = TEM-vågens strålningsstyrka omedelbart framför antennen.

    Absorptionsarean kan vi tolka som en omedelbart framför antennen och vinkelrät mot maximalstrålningsriktningen inlagd yta, var storlek är sådan, att den effekt, som passerar ytan (d.v.s. S ⋅ A, där S = strålningsstyrkan hos den infallande vågen), blir lika med den till den anpassade belastningen förda effekten. Se härtill fig. J3.17.

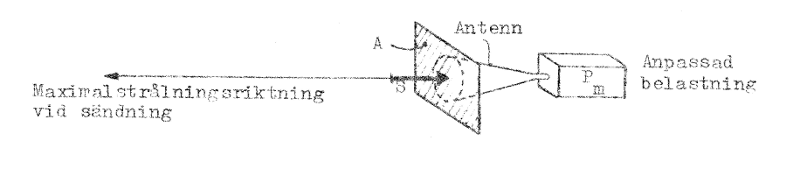	En antenns absorptionsarea Fig. J3.17

    Mellan antennförstärkningen G och absorptionsarean A råder ett i antennsammanhang synnerligen viktigt generellt samband, nämligen

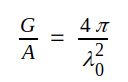J3.64

där λ₀ = våglängden (fria våglängden).

    Vid mycket hög radiofrekvens (mikrovågsområdet) är strålningsverkningsgraden η_s hög, varför i detta fall G ≈ D. Vid mycket hög radiofrekvens kan vi alltså sätta

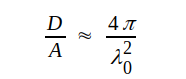J3.65

    Sambandet J3.64, som vi inte kan härleda här, utsäger bland annat, att en antenn, som ger stor strålningsstyrka i en viss riktning vid sändning, även ger stor utsignal till mottagaren, då antennen användes för mottagning från denna riktning, vilket hänger samman med den förut nämnda reciprociteten.

    I fråga om trådformiga antenner, där vi med lätthet kan definiera antennens matningsklämmor och matningsström I_eff, definierar vi antennens strålningsresistans R_s genom sambandet

J3.66

    Strålningsresistansen R_s är sålunda den resistans, som förbrukar lika mycket effekt som antennen utstrålar, då resistansen för samma ström som antennen.

    En antenn kan givetvis ha såväl reaktans X som förlustresistans R_f. En antenn med definierade matningsklämmor A och B bör sålunda kunna

		beskrivas med ett ekvivalent schema i enlighet med fig. J3.18.     Vid sändning (A-B till sändaren) representerar effekten i Rs den av antennen utstrålade effekten Ps.
Fig. J3.18

    Vid mottagning (A-B till mottagaren) får vi tänka oss en emk (i antennen inducerad emk) i serie med R_s, som då får ses som denna generators (emk:s) inre resistans.

    Låt oss slutligen beröra begreppet strålningsdiagram. Om vi på konstant avstånd från antennen i olika riktningar (α) i ett visst plan uppmäter strålningsstyrkan S, kan vi med ledning av dessa mätningar rita

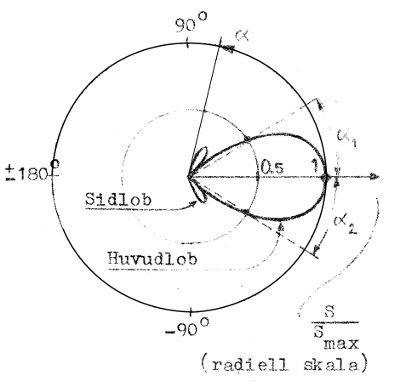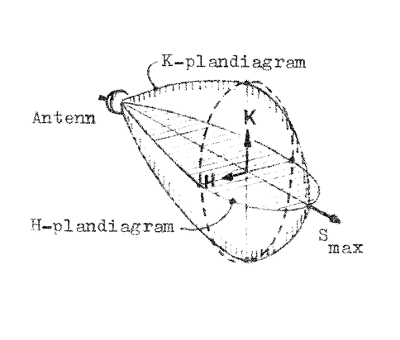
		ett polärt diagram, i vilket vi i radiell riktning avsätter S/Smax, där Smax = strålningsstyrkan i maximala strålningsriktningen. Vi får då ett s.k. strålningsdiagram i enlighet med fig. J3.19. Eftersom en antenn oftast har olika strålningsegenskaper i olika plan, brukar man rita två diagram, upptagna i två mot varandra vinkelräta plan (vanligen K-planet och H-planet, d.v.s. de plan i vilka den elektriska respektive den magnetiska fältstyrkan ligger). Vi talar om K-plandiagram och H-plandiagram. Se härtill
Strålningsdiagram Fig. J3.19

fig. J3.20. Det bör anmärkas, att diagrammen oftast ritas med den radiella storheten │K│/│K│_max i stället för som här S/S_max.

    Begreppen huvudlob och sidolob torde framgå av fig. J3.19. Vinkel-

		avståndet mellan de riktningar, i vilka strålningsstyrkan nedgått till hälften (jämför med Smax) benämns lobvinkel (α1 och α2 i fig. J3.19).     Som av prespektivskissen fig. J3.20 framgår kan lobvinkeln ha mycket olika värden i K- och H-planet beroende på det ändamål, för vilken antennen är dimensionerad.     Det bör till ånyo betonas, att detta antennavsnitt endast avser
Perspektivskiss av K- och H-planets strålningsdiagram Fig. J3.20

att vara en kortfattad orientering om några inom antenntekniken viktiga begrepp. Ett närmare studium av antenner sker i annat sammanhang.

link >