< link link link >

Vi utgår från uttrycken för fältkomponenterna för en i x-riktningen fortskridande TEM-våg, sambanden J3.24-27 (sid. J3.6), som upprepas här.

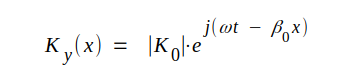	J4.1
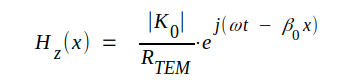	J4.2

Motsvarande momentanvärden är:

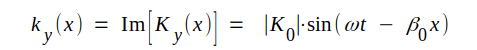	J4.3
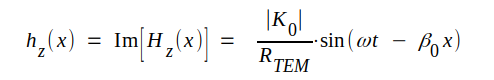	J4.4

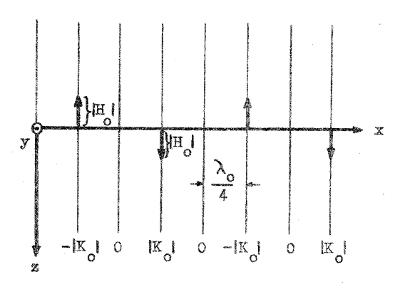
I fig. J3.6 (sid. J3.7) har vi representerat sambanden J4.3 och J4.4 vid en viss tid t = t₀, som för enkelhets skull valts lika med noll. Läsaren jämför lämpligen fig. J3.6 med vidstående fig. J4.1 och tänker därefter

		efter igenom representationen enligt fig. J4.2, där fältet utseende vid ovannämnda tidpunkt representerats med ett antal på avståndet λ₀ / 4 från varandra belägna vågfronter och på varje vågfront har motsvarande elektriska fältstyrkas storlek antecknats. Därvid har beteckningen │K₀│ använts, då fältstyrkevektorn pekar uppåt (upp mot läsaren) och - │K₀│ , då vektorn pekar nedåt. Vidare har magentiska fältstyrkan till storlek och riktning inlagts i vågfronterna. Låt oss, efter det att representationssättet enligt fig. J4.2 ordentligt genomtänkts, antaga att två lika starka TEM-vågor har utbredningsriktningarna
Fig. J4.1

Fig. J4.2

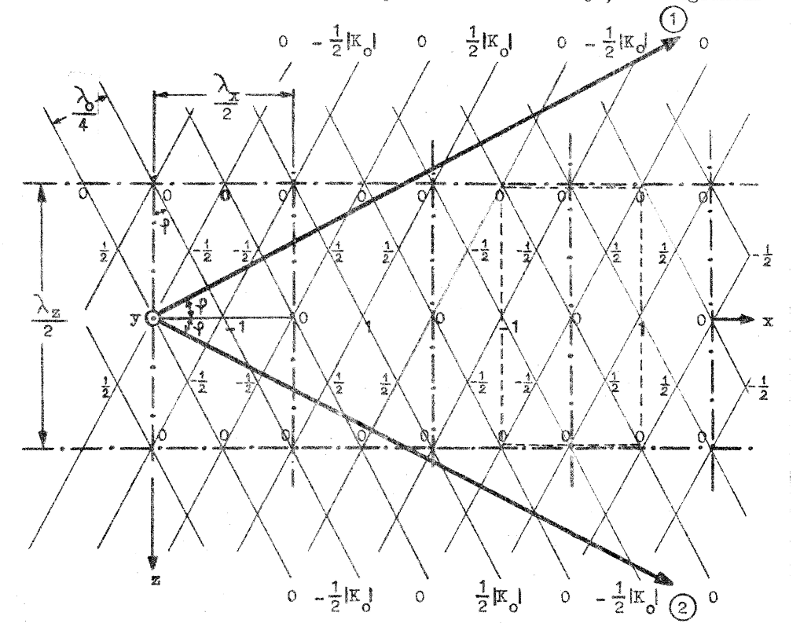
① och ② , vilka båda antages ligga i x-z-planet. Vardera utbredningsriktningen antages bilda vinkeln φ med x-axelns positiva riktning i enlighet med medanstående fig. J4.3. I vardera vågen antages den elektriska fältstyrkans toppvärde vara 1/2│K₀│ (i motsats till fig fig. J4.1 och J4.2, där fältstyrkans toppvärde antagits vara │K₀│). Vi söker nu det vågmönster, som erhålles genom interferens, när de båda TEM-vågorna överlagras. Använder vi representationssättet enligt fig. J4.1 för de enskilda vågorna, får vi ett rutnät enligt fig. J4.3.

Den elektriska fältvektorn är överallt riktad vinkelrätt och papperets plan, d.v.s. den resulterande elektriska fältstyrkan erhålles som algebraiska summan av delfältens elektriska fältstyrkor. I de utritade vågfronternas skärningspunkter (egentligen vertikala skärningslinjer) kan det elektriska fältets styrka antaga värdena 0, │K₀│ och 1/2│K₀│ och fältvektorn kan vara riktad uppåt eller nedåt. De nämnda värdena har if fig. J4.3 angivits i skärningspunkterna genom sifferbeteckningarna 0, 1, 1/2, om fältet är riktat upp från papperets plan. Är fältet nedåtriktat har sifferbeteckningarna -1 och -1/2 använts. Ett studium av fig. J4.3 visar, att elektriska fältstyrkan är noll överallt på de vertikalplan, som går genom figurens punkt-streckade linjer. Dessa linjer indelar figuren i ett antal rutor och i varje ruta har den elektriska fältstyrkan sitt största värde │K₀│ i rutans mitt och den är riktad uppåt eller nedåt. Tänker vi oss fältstyrkevektorernas "icke pilförsedda ändar" vilande mot x-z-planet, så kommer enveloppen till fältstyrkevektorernas "piländar" att bilda en yta, som påminner om ena sidan av en kudde, vars rektanguläraomkrets är fastsatt utefter den punkt-streckade linje, som begränsar rutan.


	Superponering av två TEM-vågor med gångriktningarna ➀ och ➁. Fig. J4.3

Läsaren bör nu på egen hand i fig. J4.3 rita in delvågornas magnetiska fältstyrkor i enlighet med fig. J4.2 och därefter i varje skärningspunkt rita in den resulterande magnetiska fältstyrkan (vektoriell addition). Man bör då finna, att den resulterande magnetiska fältstyrkan överallt på den streckade rektangeln i fig. J4.3 går utefter retangelsidan med en och samma omloppsriktning, varav följer att de magentiska fältlinjerna inom den streckade rutan måste bilda slutna kurvor.

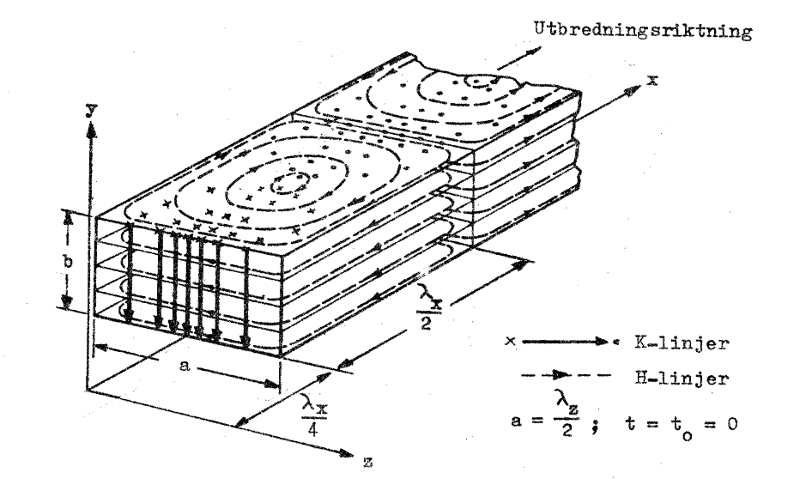
Om vi ur fältbilden i fig. J4.3 skär ut en i x-riktningen lång "låda" med viss höjd b (i y-riktningen) och med bredden a, där a är avståndet mellan de båda horisontella punkt-streckade linjerna (detta avstånd betecknas i fig. J4.3 med λ_z/2), bör vi få den bild, som fig. J4.4 söker beskriva.


	Försök till perspektivisk beskrivning av fältet i fig. J4.3 Fig. J4.4

     Observera i fig. J4.3 och J4.4 att fältets utseende vid en viss tidpunkt (t= t₀ = 0) beskrives. Om tiden går kommer delvågorna att med konstant hastighet (ljushastigheten i mediet i fråga) förskjutas i ➀- respektive ➁-riktningen, vilket innebär, att hela rutmönstret förskjutes i x-riktningen. De med z-axeln parallella punkt-streckade linjerns (planen) förskjutes i x-riktningen medan de med x-axeln parallella linjerna (planen) förblir stillastående.

    Enligt fig. J4.4 har den magnetiska fältvektorn komponenter i såväl x- som z-riktningen och endast den elektriska fältvektorn är vinkelrät mot den nya utbredningsriktningen (x-riktningen). Det resulterande fältet är alltså transversellt elektriskt och vågen benämnes därför en TE-våg. Eftersom vågtypen har en magnetisk fältstyrkekomponent i utbredningsriktningen benämnes den stundom H-våg.

    Av fig. J4.3 och fig. J4.4 framgår att sträckan λ_x utgör en komplett fältperiod i rummet i x-riktningen, varför vi med λ_x bör mena våglängden mitt i x-riktningen och analogt med λ_z våglängden mätt i z-riktningen.

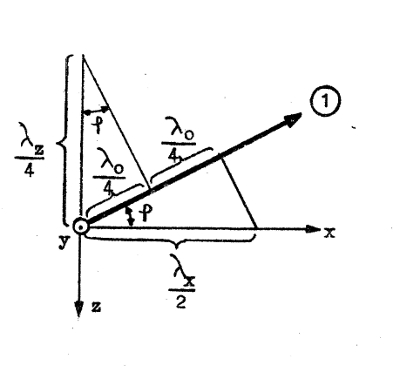		Vidstående fig. J4.5 är en delfigur, som täcker området kring y-axeln i fig. J4.3. studerar vi figurens båda trianglar finner vi för den övre, att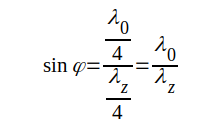 och för den nedre att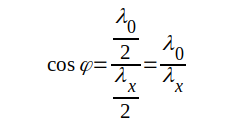
Fig. J4.5

Eftersom cos²φ + sin²φ = 1, följer av dessa båda samband att

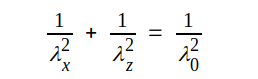J4.5

Av sambandet J4.5 följer, att såväl λ_x som λ_z är större än λ₀. λ₀, som TEM-våglängden, benämner vi i fortsättningen fri våglängd.

Vi inför storheterna β_x och β_z genom följande definitioner:

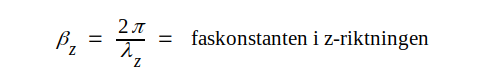Av sambandet J4.5 följer därmed, att

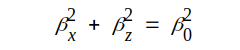J4.6

där

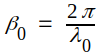= TEM-vågens faskonstant.

link >