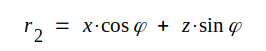< link link link >

    För den matematiskt intresserade härleds nedan uttrycken för TE-vågens fältkomponenter.

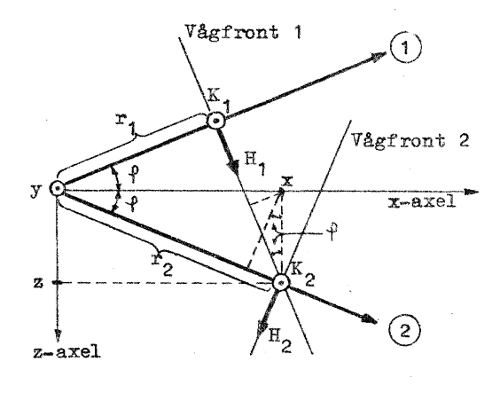
    I fig. J4.7 har utbredningsriktningarna ① och ② för våra TEM-vågor återigen utritats och vidare har för vardera vågen en vågfront angivits. De båda vågfronterna skär varandra utefter en vertikal linje, som passerar x-z-planet i punkten x, z. De båda vågfronternas avstånd till y-axeln är r₁ och r₂ respektive. Figuren avser en viss tidpunkt t.

    I analogi med sambanden J4.1 och J4.2 kan fältstyrkorna i våra delfält i komplex form skrivas på följande sätt.

Våg ①		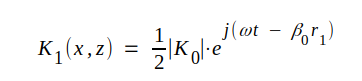J4.11
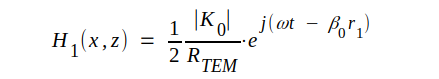		J4.12

Våg ②		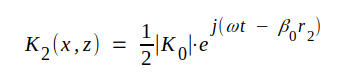J4.13
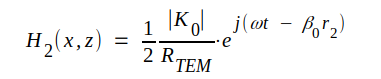		J4.14

    Vi observerar, att elektriska fältstyrkeamplituden antagits vara ½│K₀│(i motsats till sambanden J4.1-4 men i överensstämmelse med våra antaganden i samband med fig. J4.3). Våra fält är funktioner av x och z (och givetvis t), eftersom r₁ och r₂ är funktioner av x och z.

		Projicerar vi sträckorna x och z på r1- och r2-riktningarna får vi sambanden J4.15 J4.16     Det elektriska fältet är överallt parallellt med y-axeln, varför det totala elektriska fältet i punkten x,z blir (index x, y och z utmärker respektive komponenters riktningar):
Fig. J4.7

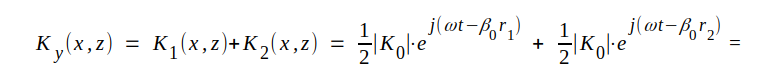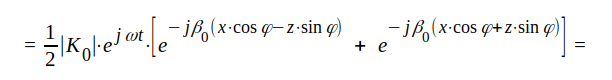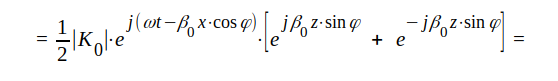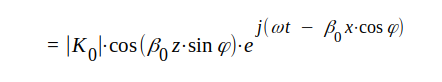J4.17

    Enligt sambanden på sid. J4.5 har vi följande uttryck på sinφ och cosφ.


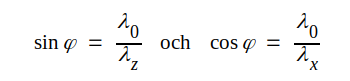   Vi får sålunda (se även sid. J4.5):


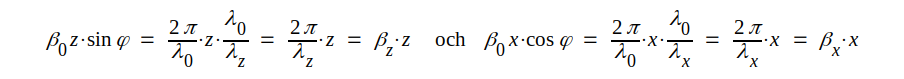    Insättning av dessa uttryck i sambandet J4.17 ger

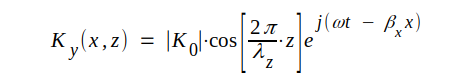J4.18

    Totala magnetiska fältstyrkan har tydligen komponenter i både x- och z-riktningen och ur fig. J4.7 får vi för z-komponenten


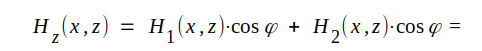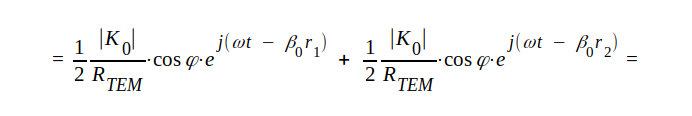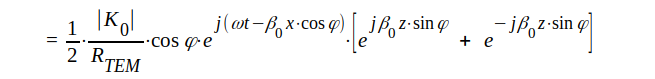    Den fortsatta räkningen följer helt det räkneschema, vi använt ovan vid härledningen av Ky(x.z), varför det överlåtes åt läsaren att kontrollera slutresultatet:

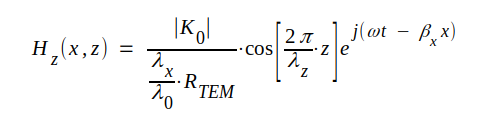J4.19

    För totala H-fältets komponent i x-riktningen erhålles med ledning av fig. J4.7


    Det överlåtes åt läsaren att genomföra den att genomföra den fortsatta beräkningen och därmed visa att

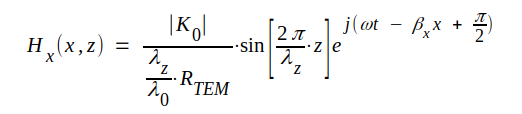J4.20

    Fältkomponenternas ögonblicksvärden erhålles nu lätt ur sambanden J4.18, J4.19 och J4.20.

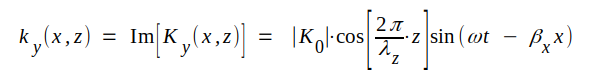	J4.21
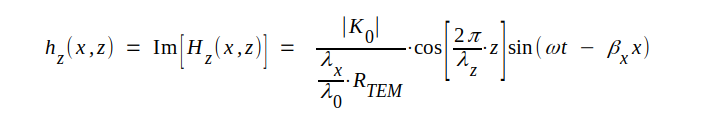	J4.22
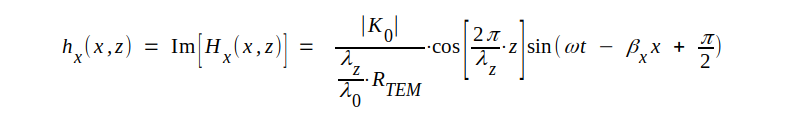	J4.23

Övning: Sätt t=0 i sambanden J4.21-23, jämför med fig. J4.3 och kontrollera överensstämmelsen mellan figur och samband.

    Observera att fältkomponenterna vinkelrätt mot utbredningsriktningen [K_y(x,z) och H_z(x,z)] är i fas med varandra medan komponenten i utbredningsriktningen H_x(x,z) är 90° ur fas relativt de transversella komponenterna, något som för övrigt kan inses genom studium av fig. J4.3.

    I analogi med TEM-vågen definierar vi TE-vågens komplexa vågimpedans (eller här alternativt vågresistans) som kvoten mellan de transversella komplexa komponenterna d.v.s.

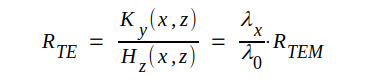J4.24

    Observera speciellt det ur minnessynpunkt behagligare uttrycket

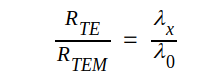J4.25

link >