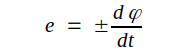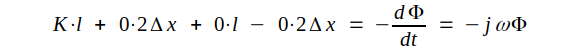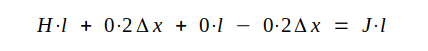Införs ett främmande material (metall eller dielektrikum) i ett elektromagnetiskt fält, påtvingar vi fältet vissa randvillkor, d.v.s. fältet i materialytan (metallytan) kan ej anta vilka värden som helst.
Vi diskuterar i detta avsnitt endast materialet metall och förutsätter därvid tills vidare, att metallen är ideal, d.v.s. metallens konduktivitet δ = ∞ . Under denna förutsättning kan ett växelfält ej tränga in i metallen på grund av uppkomsten av ett lika starkt men motriktat, inducerat fält. Metallens inre blir ett fältfritt område och eventuell ström i metallen blir en ren ytström, koncentrerad till ett oändligt tunt strömskikt i metallytan.
Låt oss exempelvis anta att ett magnetiskt flöde φ passerar igenom
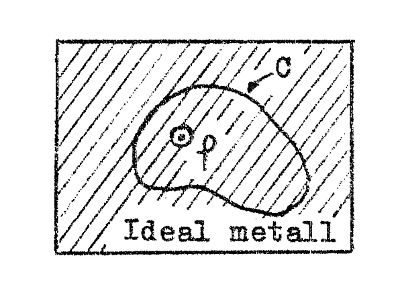 |
konturen C, belägen inuti en
ideal metall. Enligt induktionslagen induceras då längs
konturen en emk:
Enär metallen antagits ha resistiviten noll (δ = ∞), kan någon potentialskilland ej |
||||
| Fig. J4.8 |
existera mellan två punkter i metallen. Alltså har vi e = 0, vilket betyder att φ = 0 eller φ = konstant, detta sista givetvis ej aktuellt i fråga om växelfält. Både φ och e är alltså lika med noll, vilket innebär, att varken elektrisk eller magnetisk fältstyrka kan existera inuti en ideal metall. Det är detta förhållande vi utnyttjar, då vi med skärmburkar skärmar mot elektromagnetiska fält (jämför sid. B7.11 i Kompendium del IB).
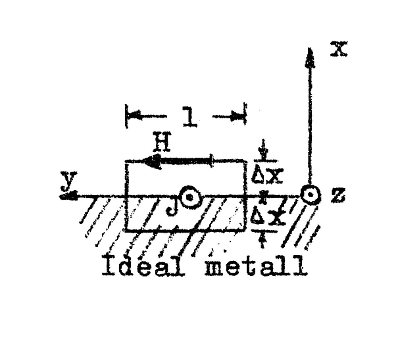
Antag nu att ett elektromagnetiskt fält har sin elektriska fältstyrka riktad parallellt med ytan på en ideal metall (fig. J4.9). Induktionslagen
 |
ger då för den rekatangulära
konturen C:
där K och Φ är komplex elektrisk fältstyrka respektive komplext magnetiskt flöde enligt fig. J4.9. |
|||
| Ideal metall Fig. J4.9 |
Låter vi Δx → 0, kommer K att betyda elektriska fältstyrkan i metallytan. Φ är ändlig, varför, när Δx → 0, det av konturen omslutna flödet blir noll, d.v.s. K ⋅ l = 0 eller med andra ord K = 0.
Vi har allstså dragit följande viktiga slutsats
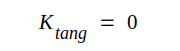 |
J4.26 |
där vi infört index tang för att utmärka en i den ideala metallytan liggande och tangentiellt till denna riktad fältstyrka.
Av sambandet J4.26 följer att en magnetisk fältstyrka ej kan vara vinkelrät mot en ideal metallyta. Vore den vinkelrät, skulle vi ha ett magnetiskt flöde vinkelrätt mot metallytan, vilket enligt induktionslagen skulle innebära en till metallytan tangentiell elektrisk fältstyrka, något som vårt nyss härledda samband J4.26 förbjuder.
Alltså har vi
| J4.27 |
där vi infört index norm för att utmärka en vinkelrätt (normalt) mot den ideala metallytan riktad fältstyrka.
 |
Slutligen
antar vi en magnetisk fältstyrka i metallytans riktning
och gör med ledning av fig. J4.10 en undersökning av
detta fall. Vi tillämpar Ampere's lag, som på grund av
sambandet J4.26 kan anses gälla vid gränsövergången
nedan. Vi får
|
|||
| Ideal metall Fig. J4.10 |
där J = ytströmmen per längdenhet (längdenheten givetvis tagen vinkelrätt mot strömriktningen).
Efter gränsövergång Δx → 0 erhålles
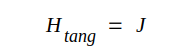 |
J4.28 |
Sambandet J4.28 visar, att magnetiska tangentiella fältstyrkans amplitud och fas är desamma som ytströmtäthetens amplitud och fas, men vi får inte glömma att vektorn ℋ och vektorn ℑ, som båda ligger i metallytan är vinkelräta mot varandra.
Randvillkoren J4.26, 27 och 28 är av största betydelse för vårt fortsatta studium av bl.a. vågledare. Det bör dock ihågkommas, att randvillkoren ovan avser en metall med oändligt god ledningsförmåga. En dylik metall existerar ej, men en god ledare (koppar, silver) är i många fall med god approximation en ideal metall.
Villkoret J4.26 innebär, att den elektriska fältstyrkan vid ytan av en ideal metall antingen är noll eller är riktad vinkelrätt mot metallytan. Om metallens ledningsförmåga är stor men ändlig, måste en viss liten elektrisk fältstyrka finnas i metallytan, vilket i sin tur innebär, att det totala elektriska fältet bildar en viss liten vinkel med normalen till metallytan. Till dessa frågor får vi anledning återkomma.
link >