< link link link >

    Vi skall nu undersöka laddnings- och strömfördelningen i vågledarväggen. Eftersom vi antagit, att vågledaren är tillverkad av ideal metall, är såväl laddning som ström enligt tidigare utredning koncentrerad till ytskiktet av vågledarväggens insida.

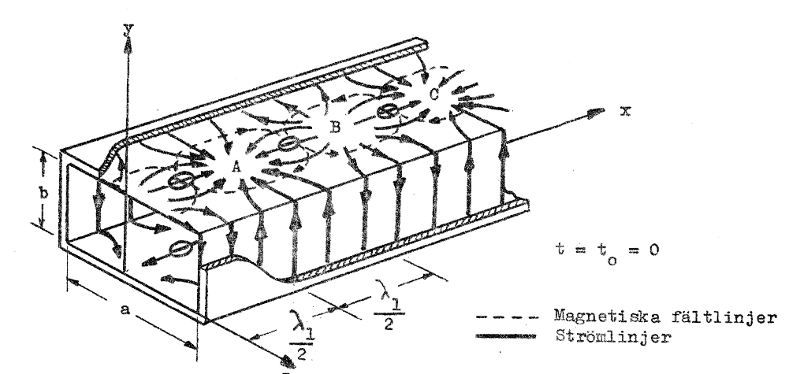
    Laddningstätheten är störst, där elektriska flödestätheten är störst d.v.s. där elektriska fältstyrkan är störst. Dessa punkter har i fig. J4.12 utmärkts med ⊕ och ⊖ (+ för positiv och - för negativ laddning). Strömriktningen i vågledarytan måste i enlighet med överläggningen på sid. J4.11 överallt vara vinkelrät mot H-linjerna i väggen. Se härtill fig. J4.12, som ritats vid tidpunkten t = t₀ = 0, d.v.s.vid samma tidpunkt som i fig. J4.3 (sid. J4.3). Det är därför lämpligt att jämföra dessa båda figurer.

    Låter vi t öka, kommer hela fält-, laddnings- och strömbilden i fig. J4.12 att med fashastigheten förflyttas i x-riktningen.


	Försök till beskrivning av strömbilden i vågledarens inneryta. Några få magnetiska fältlinjer i vågledarens övre inneryta har utritats. Vågledaren är delvis uppskuren, men "innerytan" finns kvar efter uppskärningen. Figuren är orienterad i x-y-z-systemet på samma sätt som i fig. J4.3. Figuren visar strömlinjernas förlopp vid tidpunkten t=t₀=0. Fig. J4.12

Eftersom alla strömlinjer i övre vågledarytan går in mot punkten A, (respektive ut från punkten B) in mot punkten C o.s.v. kanske vi frågar oss vart strömmen i dessa punkter tar vägen. Vi kan tänka oss strömlinjerna slutna tvärs över vågledaren från t.ex. området A till motsvarande område i vågledarens bottenyta. Denna hypotetiska ström benämner vi efter Maxwell förskjutningsström (kondensatorström). I växelströmsteorien talar vi ofta om strömmen genom en kondensator utan att därför mena, att laddning "hoppar" över från ena kondensatorplattan till den andra.

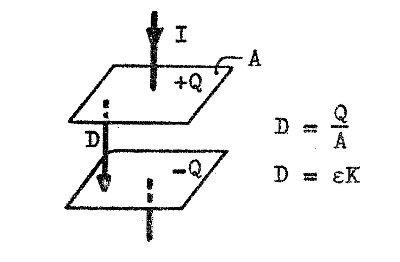		Låt oss betrakta en plan kondensator med plattarean A enligt vidstående fig. J4.13, där den homogena elektriska flödestätheten betecknas med D (kondenstatorns randeffekter lämnas utan avseende): Strömmen till kondensatorn blir i komplex form
Fig. J4.13

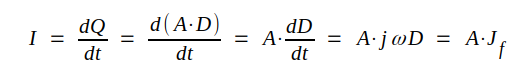J4.50

Faktorn

(eller i komplex form jωD) har dimensionen A/m² och kan uppfattas som strömmen per ytenhet genom kondensatordielektrikum. Vi säger, att strömmen i kondensatorns tilledning är en ledningsström medan strömmen genom själva kondensatorn är en förskjutningsström.

På liknande sätt blir förskjutningsströmtätheten J_fy utefter en linje mellan vågledarens övre och undre yta:

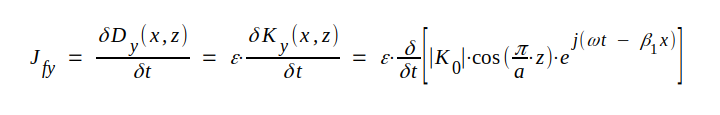	eller
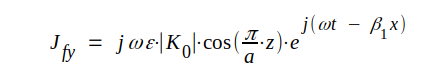	J4.51

Motsvarande momentanvärde blir:

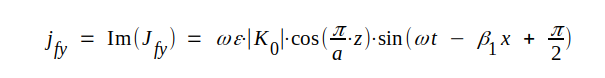J4.52

Vid tiden t = 0 (som fig. J4.12 avser) blir J_fy störst, då vi väljer z = 0 och -β_lx + π/2 = π/2 ± n·π ( n=0, 1, 2, 3, ...) d.v.s. för

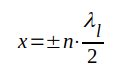Dessa x-värden representerar som väntat just punkterna A, B, C o.s.v. i fig. J4.12.

Med ledning av sambandet J4.28 samt sambanden J4.36 och J4.38 får vi för komplexa ytströmtätheten i vågledarens övre inneryta (y = b) följande uttryck:

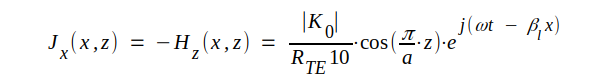	J4.53
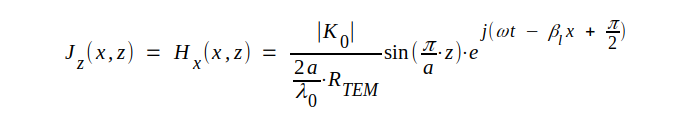	J4.54

För ytströmtätheteskomponenterna i vågledarens nedre inneryta (y = 0) gäller samma uttryck med ombytt tecken.

För ytströmtätheten i högra innerväggen (z = a/2) fås på liknande sätt

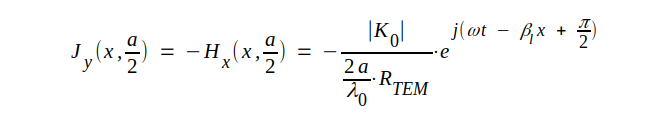J4.55

För andra innerväggen (z = - a/2) gäller samma uttryck med ombytt tecken.

		Vidstående fig. J4.14 får klargöra innebörden av ytströmstorheterna J_x, J_y och J_z.
Fig. J4.14

link >